Introduction
One of the best ways to sharpen your Java skills is to tackle classic algorithmic problems. A perfect starting point is creating a prime number program in Java—an exercise that is essential for mastering loops, conditional statements, and logical thinking.
This tutorial is here to help you succeed. We'll start from the basics, showing you how to build a simple prime number program in Java using various methods. From for loops to more optimized techniques, you'll learn everything you need to write effective and efficient code for this common challenge. Let's get started!
Mastering concepts like the switch statement is a great start. Ready to build powerful, real-world applications? Explore our Online Software Engineering Courses to gain expertise in core Java, advanced data structures, and industry best practices. Launch your developer career today!
Overview
Any natural number that is greater than 1 and divisible by 1 and itself only is termed a prime number. The isPrime() function is usually used in Java to determine whether the input number is prime or not.
What are Prime Numbers?
All natural numbers can be categorized into 2 classes ⎯ prime numbers and composite numbers.
A prime number is defined as a natural number greater than 1 which is divisible by 1 and the number itself only. It has only 2 divisors. Some examples of prime numbers are 2,3,5,7,13,47,53…
On the other hand, composite or non-prime numbers are divisible by more than 2 numbers apart from 1 and itself.
If you're looking to master core Java concepts like the prime number and build a strong foundation in programming, here are some top-rated courses from upGrad to help you get there:
Some interesting facts about Prime Numbers
- 0 and 1 are neither prime nor composite numbers.
- The only consecutive natural prime numbers are 2 and 3.
- No prime number greater than 5 ends in 5. This is because all numbers ending with 5 are divisible by 5 besides the number itself.
- Twin prime numbers are consecutive primes that come with a composite number between them. Their difference is always. Example - (5,7), (11,13), (17,19), (29,3,), (41,43), (59,61), (71,73).
- 17 and 71 are called twisted prime numbers as both are prime and mirror images of each other. Other examples - (13,31), (37,73), (79,97).
Properties of Prime Numbers
- All numbers greater than 1 can be divided by at least one prime number.
- 2 is the smallest as well as the only even prime number. All other prime numbers are odd.
- All prime numbers except 2 and 3 can be represented in the form of either 6n+1 or 6n-1. (n= any natural number)
- Any given positive integer that is greater than 2 can be written as a sum of two prime integers.
- Two prime numbers are always coprimes of one another.
- Any given composite number can be divided into prime factors, which individually are unique.
Prime Numbers and Co-prime Numbers
Prime and co-prime numbers are distinctly different.
Prime Numbers | Co-prime Numbers |
Single number | Always come in pairs. |
Only factors are 1 and itself. | Highest common factor is always 1. |
Only primes. | Can be prime or composite. |
Examples - 17,23,67 | Examples- (17,25), (6,13), (8,15) |
How to check whether a number is Prime or not?
We will be using the ‘isPrime’ method for finding out if a number is prime or not in the following program. However, in this method, you must name the .java file where you are writing the code as ‘PrimeCheker.java’ or it will cause an error during compilation.
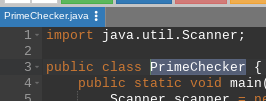
If the ‘PrimeChecker’ class is not declared in a PrimeChecker.java file, it will cause the following error after execution:
Here is the program:
import java.util.Scanner;
public class PrimeChecker {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("Enter a number to check Prime or Not: ");
int number = scanner.nextInt();
if (isPrime(number)) {
System.out.println(number + " is a prime number");
} else {
System.out.println(number + " is not a prime number");
}
}
private static boolean isPrime(int number) {
if (number <= 1) {
return false;
}
for (int i = 2; i <= Math.sqrt(number); i++) {
if (number % i == 0) {
return false;
}
}
return true;
}
}
The prime number program in javascript begins with importing the Scanner class from java.util package using “import java.util.Scanner;”. Next, an instance of the Scanner class is created using “Scanner scanner = new Scanner(System.in);” which allows users to input a number. This is followed by the program prompt “System.out.print("Enter a number to check Prime or Not: ");”.
The program reads the user’s input using the “scanner.nextInt()” method. The entered number’s value is stored in an integer variable termed “number” using “int number = scanner.nextInt();”. The isPrime() method with the entered value is called an “argument” which checks whether the number is prime or not.
If the java program to print prime numbers in a given range returns true with the statement flashing “System.out.println(number + " is a prime number");” then the entered value is prime. If not, the isPrime() method returns false with the message “System.out.println(number + " is not a prime number");”. This indicates the entered value is not prime.
Prime Number Program using checkPrime Method in Java
public class prime{
static void checkPrime(int a){
int i,m=0,flag=0;
m=a/2;
if(a==0||a==1){
System.out.println(a+" is not prime number");
}else{
for(i=2;i<=m;i++){
if(a%i==0){
System.out.println(a+" is not prime number");
flag=1;
break;
}
}
if(flag==0) { System.out.println(a+" is prime number"); }
}
}
public static void main(String args[]){
checkPrime(10);
checkPrime(45);
checkPrime(67);
checkPrime(15);
}
}
Another way to write a program to check if a given number is prime or not is by using the “checkPrime” method. The checkPrime method takes an integer “a” as input and declares its variables “i,” “m,” and “flag” to 0. The value of “m” is set to “a/2,” and the program prints "a is not a prime number" when the variable is equal to 0 or 1. The program then enters a “for” loop that initializes “i” to 2 and continues until “i” is less than or equal to “m.”
Among the given inputs, only 67 returns as prime.
Prime Number Program in Java (Another way)
In the following program, we will be using the Lucas-Lehmer test for Mersenne primes to find out if a number is prime or not.
import java.math.BigInteger;
import java.util.Scanner;
public class PrimeChecker {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("Enter a number to check Prime or Not: ");
int number = scanner.nextInt();
BigInteger mersenneNumber = BigInteger.valueOf(2).pow(number).subtract(BigInteger.ONE);
BigInteger s = BigInteger.valueOf(4);
for (int i = 3; i <= number; i++) {
s = s.multiply(s).subtract(BigInteger.valueOf(2));
s = s.mod(mersenneNumber);
}
if (s.equals(BigInteger.ZERO)) {
System.out.println(number + " is a prime number");
} else {
System.out.println(number + " is not a prime number");
}
}
}
Find prime numbers between two numbers
import java.util.Scanner;
public class prime {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.print("Enter the source number : ");
int source = sc.nextInt();
System.out.print("Enter the destination number : ");
int destination = sc.nextInt();
System.out.println("List of prime numbers between " + source + " and " + destination);
for (int i = source; i <= destination; i++) {
if (isPrime(i)) {
System.out.println(i);
}
}
}
public static boolean isPrime(int n) {
if (n <= 1) {
return false;
}
for (int i = 2; i <= Math.sqrt(n); i++) {
if (n % i == 0) {
return false;
}
}
return true;
}
}
How We Check Whether a Number is Prime or Not?
In the following program, we will use the Sieve of Eratosthenes method to determine if a number is prime.
import java.util.Scanner;
public class PrimeChecker {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("Enter a number to check Prime or Not: ");
int number = scanner.nextInt();
boolean[] isPrime = new boolean[number + 1];
for (int i = 2; i <= number; i++) {
isPrime[i] = true;
}
for (int i = 2; i * i <= number; i++) {
if (isPrime[i]) {
for (int j = i * i; j <= number; j += i) {
isPrime[j] = false;
}
}
}
if (isPrime[number]) {
System.out.println(number + " is a prime number");
} else {
System.out.println(number + " is not a prime number");
}
}
}
Program to Check Prime Number Using a For Loop
import java.util.Scanner;
public class PrimeChecker {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.print("Enter a number to check Prime or Not: ");
int number = scanner.nextInt();
int count = 0;
for (int i = 2; i <= number / 2; i++) {
if (number % i == 0) {
count++;
break;
}
}
if (count == 0) {
System.out.println(number + " is a prime number");
} else {
System.out.println(number + " is not a prime number");
}
}
}
Program to Check Prime Number Using a While Loop
import java.util.Scanner;
public class prime {
public static void main(String[] args) {
System.out.println("Enter a number to check Prime or Not");
Scanner obj = new Scanner(System.in);
int p = obj.nextInt();
int i = 2, c = 0;
while (i <= p / 2) {
if (p % i == 0) {
c++;
break;
}
i++;
}
if (c == 0) {
System.out.println(p + " is prime number");
} else {
System.out.println(p + " is not a prime number");
}
}
}
Program to Check If the Number is Prime or not using a Flag Variable
import java.util.Scanner;
public class prime {
public static void main(String args[]){
int i,a=0,flag=0;
Scanner myObj = new Scanner(System.in);
System.out.println("Enter a number");
int n = myObj.nextInt();
System.out.println("the number is: " + n);
a=n/2;
if(n==0||n==1){
System.out.println(n+" is not prime number");
}else{
for(i=2;i<=a;i++){
if(n%i==0){
System.out.println(n+" is not prime number");
flag=1;
break;
}
}
if(flag==0) { System.out.println(n+" is prime number"); }
}
}
}
Further Optimization
Let us now further optimize the above code by using a boolean variable ‘isPrime’ rather than a flag variable. The boolean variable will help us determine if the number is a prime number or not, based on the value of ‘isPrime’.
import java.util.Scanner;
public class PrimeChecker {
public static void main(String args[]) {
int i, limit;
boolean isPrime = true;
Scanner scanner = new Scanner(System.in);
System.out.print("Enter a number: ");
int number = scanner.nextInt();
if (number == 0 || number == 1) {
System.out.println(number + " is not a prime number");
return;
}
limit = (int) Math.sqrt(number);
for (i = 2; i <= limit; i++) {
if (number % i == 0) {
isPrime = false;
break;
}
}
if (isPrime) {
System.out.println(number + " is a prime number");
} else {
System.out.println(number + " is not a prime number");
}
}
}
Program to Display the prime Numbers From 1 to 100
import java.util.Scanner;
public class prime {
public static void main(String[] args) {
System.out.println("Enter a number range to generate prime numbers in between");
Scanner obj = new Scanner(System.in);
int n1 = obj.nextInt();
int n2 = obj.nextInt();
if (n1 >= n2) {
System.out.println("Number2 must be greater then number1");
System.exit(0);
}
while (n1 <= n2) {
int i = 2, count = 0;
while (i <= n1 / 2) {
if (n1 % i == 0) {
count++;
break;
}
i++;
}
if (count == 0) {
System.out.println(n1 + " is prime number");
}
n1++;
}
}
}
To print prime numbers from 1 to 100 in Java, the program reads in two integer values from the user 1 and 100. An “if” statement checks if the first number is greater than or equal to the second.
Find Prime Number Using Recursion
class prime {
static boolean isPrime(int p, int i) {
if (p <= 2) return (p == 2) ? true : false;
if (p % i == 0) return false;
if (i * i > p) return true;
return isPrime(p, i + 1);
}
public static void main(String[] args) {
int a = 11;
if (isPrime(a, 7)) {
System.out.println("The number is prime");
}
else {
System.out.println("The number is not prime");
}
}
}
Conclusion
Mastering the logic behind the prime number program in Java is a crucial milestone for any new developer. It’s more than just a simple exercise; it’s a practical way to solidify your understanding of core concepts like loops and conditional statements.
By building and optimizing a prime number program in Java, you're not just learning to solve one problem, you're learning how to think like a programmer. Keep practicing with these foundational challenges, and you'll be well-prepared for a successful coding career.
FAQs
1. What is a prime number, and what is the basic logic to check for one?
A prime number is a natural number greater than 1 that has exactly two distinct positive divisors: 1 and itself. For example, 7 is a prime number because it can only be divided by 1 and 7. The number 6 is not prime because it is divisible by 1, 2, 3, and 6. The basic logic for a prime number program in Java involves checking if a given number n has any divisors between 2 and n-1. If a divisor is found, the number is not prime; if the check completes without finding any divisors, the number is prime.
2. Is 1 a prime number in Java?
No, 1 is not a prime number. The mathematical definition of a prime number is a natural number greater than 1 that has only two divisors: 1 and itself. The number 1 only has a single divisor (itself), so it does not meet this two-divisor criterion. Any correctly written prime number program in Java should have a condition at the beginning to handle this, immediately returning false for any number less than or equal to 1.
3. How do you write a simple prime number program in Java using a for loop?
A simple prime number program in Java can be written using a for loop to perform trial division. You would create a function that takes an integer n as input. First, you handle the edge cases (numbers less than 2 are not prime). Then, you loop from i = 2 up to n-1. Inside the loop, you use the modulo operator (%) to check if n is divisible by i. If n % i == 0 at any point, you can immediately return false. If the loop finishes without finding any divisors, you can return true.
4. Why is it more efficient to check for divisors only up to the square root of the number?
This is a critical optimization for any prime number program in Java. If a number n has a divisor d that is larger than its square root (√n), then it must also have a corresponding divisor c such that d * c = n. In this scenario, c must be smaller than √n. Therefore, if a number has any divisors, at least one of them will always be less than or equal to its square root. By only checking up to √n, you dramatically reduce the number of iterations required, significantly improving your program's performance for large numbers.
5. What is the Sieve of Eratosthenes, and how is it implemented?
The Sieve of Eratosthenes is a highly efficient ancient algorithm for finding all prime numbers up to a specified limit. To implement it, you create a boolean array, say isPrime, where isPrime[i] is initially true for all numbers. You then start with the first prime, 2, and iterate through the array, marking all multiples of 2 (4, 6, 8, etc.) as false. You then find the next number that is still marked true (which will be 3) and repeat the process. This continues until you have processed all numbers up to the square root of your limit, leaving you with an array where only the prime numbers are marked true.
6. How can I write a program to print all prime numbers up to a certain number N?
The most efficient way to do this is to use the Sieve of Eratosthenes algorithm. However, a simpler, more intuitive method for a beginner is to write a helper function isPrime(num). Then, you can create a for loop that iterates from 2 to N. Inside the loop, you call your isPrime() function for each number. If the function returns true, you print the number. This is a great way to structure a simple prime number program in Java.
7. What is the difference between break and continue in a prime number checking loop?
In a loop that is checking for divisors, break and continue have very different functions. If you find a divisor (e.g., n % i == 0), you should use break. This will immediately terminate the loop because you have already proven the number is not prime, and there is no need to check further. The continue statement, on the other hand, would simply skip to the next iteration of the loop, which is not the correct logic for this problem.
8. What are some common mistakes to avoid in a prime number program in Java?
A common mistake is forgetting to handle the edge cases of 0, 1, and negative numbers. Another is setting the loop's end condition incorrectly (e.g., looping up to n instead of √n, which is inefficient). A subtle but frequent bug is incorrectly placing the return true statement inside the loop, which can cause the function to return a wrong result before all necessary checks have been completed. A good prime number program in Java must be both logically correct and efficient.
9. How can I make my prime number checking logic reusable?
To make your logic reusable, you must encapsulate it within a well-defined function. For example, create a public static method public static boolean isPrime(int number). This function should contain all the logic for checking primality and should return either true or false. By doing this, any other part of your application can check if a number is prime simply by calling this single, reliable function, which is a core principle of good software design.
10. Can a prime number program be written using recursion?
Yes, you can write a prime number program in Java using recursion, although it is less common and generally less efficient than an iterative approach due to the overhead of function calls. A recursive function would typically take two arguments: the number to check and the current divisor. The function would check for divisibility, and if no divisor is found, it would call itself with the next divisor until the divisor exceeds the square root of the number.
11. What is the time complexity of checking for a prime number?
The time complexity depends on the algorithm. A naive prime number program in Java that checks for divisors from 2 up to n-1 has a time complexity of O(n). The optimized approach, which checks only up to the square root of n, has a much better time complexity of O(√n). For generating a list of primes, the Sieve of Eratosthenes is even more efficient, with a time complexity of O(n log log n).
12. How do you handle large prime numbers in Java?
To deal with very large numbers that exceed the capacity of Java's int or long data types, you must use the BigInteger class from the java.math package. This class can handle integers of arbitrary size. BigInteger has a built-in method called isProbablePrime(), which is a highly efficient probabilistic test. It takes an argument for "certainty," and if it returns true, there is an extremely high probability that the number is prime.
13. What is a "probabilistic" primality test?
A probabilistic primality test, like the Miller-Rabin test used by BigInteger.isProbablePrime(), does not definitively prove a number is prime. Instead, it provides an answer with a certain level of probability. For a given number, it can prove with 100% certainty if it is composite, but it can only state that it is prime with a very high probability (e.g., 99.999...%). For all practical purposes, especially in cryptography, this level of certainty is sufficient.
14. What is the difference between a prime and a composite number?
A prime number is a natural number greater than 1 that has only two divisors: 1 and itself. A composite number is a natural number greater than 1 that is not prime, meaning it has at least one other divisor besides 1 and itself. For example, 7 is prime, while 9 is composite because it is divisible by 3. A prime number program in Java is essentially a tool to distinguish between these two categories.
15. Can I use Java Streams to find prime numbers?
Yes, you can use Java Streams for a more modern, functional approach. For example, to check if a number n is prime, you could use IntStream.range(2, (int) Math.sqrt(n) + 1).noneMatch(divisor -> n % divisor == 0). This creates a stream of numbers from 2 to the square root of n and checks if "none of them" divide n evenly. This is a very concise and expressive way to write a prime number program in Java.
16. Are there any libraries in Java for working with prime numbers?
While Java's standard library does not have a dedicated prime number utility class like calendar.isleap() for leap years, the BigInteger class is the standard tool for handling very large prime numbers. For more extensive number theory functionalities, developers often use third-party libraries like Apache Commons Math.
17. How are prime numbers used in real-world applications?
Prime numbers are the backbone of modern cryptography and internet security. Public-key encryption algorithms, like RSA, rely on the fact that it is easy to multiply two very large prime numbers together, but it is computationally infeasible to do the reverse (i.e., factor the large product back into its original primes). This mathematical difficulty is what keeps online transactions and communications secure.
18. Why is the prime number problem a common interview question?
The prime number program in Java is a classic technical interview question because it tests several fundamental skills at once. It assesses a candidate's understanding of basic programming constructs like loops and conditionals, their ability to translate a mathematical definition into code, and, most importantly, their grasp of optimization. The difference between a naive O(n) solution and an optimized O(√n) solution reveals a lot about a candidate's algorithmic thinking.
19. How can I learn to solve more Java programming challenges like this?
The best way to improve your problem-solving skills is through a combination of structured learning and consistent practice. A comprehensive program, like the software development courses offered by upGrad, can provide a strong foundation in Java and data structures. You should then apply this knowledge by regularly solving problems on coding platforms, which will expose you to a wide variety of challenges and help you master the logic needed for any simple prime number program in Java and beyond.
20. What is the main takeaway from learning to write a prime number program?
The main takeaway is not just about identifying a Prime Number in Python, but about learning the fundamentals of algorithmic thinking and optimization. The process of starting with a simple, brute-force solution and then refining it by applying mathematical properties (like checking only up to the square root) is a perfect example of the problem-solving mindset that is at the heart of computer science. It's a foundational exercise that teaches you how to write code that is not just correct, but also efficient.
Take the Free Quiz on Java
Answer quick questions and assess your Java knowledge
-9cd0a42cab014b9e8d6d4c4ba3f27ab1.webp&w=3840&q=75)
